DFS로 2차원 배열 탐색하기 #

2차원 배열 이해하기 #

깊이 우선 탐색으로 2차원 배열을 탐색해보겠습니다. 탐색을 한다면 어떤 목적이 있어야겠습니다.

깊이 우선 탐색으로 아래의 2차원 배열에서 1을 찾아보겠습니다. 시작은 좌표 (0, 0)에서 시작합니다.

(0, 0) = arr2D[0][0]입니다.

const arr2D = [
    [0, 0, 0],
    [0, 0, 0],
    [0, 1, 0],
]

아래와 같은 그림으로 이해 할 수 있습니다.

2차원 배열을 이동하는 DFS 이해하기 #

좌표 (0, 0)에서 부터 탐색을 시작해 아래와 같은 규칙을 통해 움직입니다.

탐색을 완료한 경우 좌표를 남긴다.
완료한 탐색의 좌표는 누적한다.
누적된 탐색의 좌표를 따라가면 마지막이 찾고자 하는 좌표이다. 찾지 못하면 null을 반환한다.

DFS 함수로 1을 찾은 경로는 아래와 같을 것입니다.

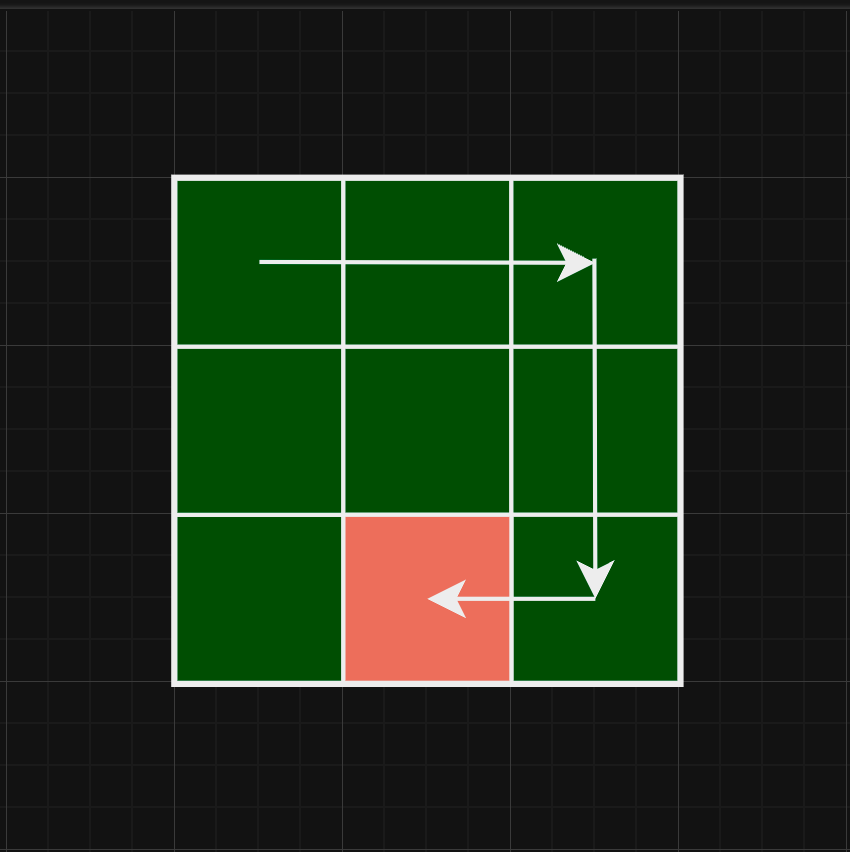
[[ 0, 0 ], // 0, 0에 있다.
 [ 0, 1 ], // 직전 좌표에서 한 칸 오른쪽으로 이동했다.
 [ 0, 2 ], // 직전 좌표에서 한 칸 오른쪽으로 이동했다.
 [ 1, 2 ], // 직전 좌표에서 한 칸 아래로 이동했다.
 [ 2, 2 ], // 직전 좌표에서 한 칸 아래로 이동했다.
 [ 2, 1 ]] // 직전 좌표에서 한 칸 왼쪽으로 이동했다.

위 좌표들은 2차원 배열을 DFS로 이동한 path 값입니다. 자세히 살펴보면 최단경로로 이동하고 있지 않다는 것을 알 수 있습니다.

이유는 DFS의 특징을 따르기 때문입니다. 이차원 배열을 뒤져보면서 갈 수 있는한 최대한 깊은 곳까지 이동하고, 막히면 다시 뒤로 돌아와 다시 탐색 경로를 찾습니다.

DFS를 구현해보기 #

1. cols, rows 선언 #

function dfs(){
  const array = [
    [0, 0, 0],
    [0, 0, 0],
    [0, 1, 0],
  ];
  const cols = array[0].length;
  const rows = array.length;
}

cols: 2차원 배열의 열의 수
rows: 2차원 배열의 행의 수

2. visited, stack의 선언 #

  const visited = Array.from({ length: rows }, () => Array(cols).fill(false));
  const stack = [[[0, 0], []]];

visited: 한번 방문한 좌표는 또 방문 할 필요가 없기에 이를 체크하기 위한 변수
stack: 이동 경로를 저장하기 위한 3차원 배열 변수
- 초기값으로 [0, 0] 좌표를 저장합니다.
- 그동안 축적될 좌표를 저장할 빈 배열도 함께 저장합니다.

3. directions | 이동 방향 설정하기 #

  const directions = [
    [-1, 0], // 위
    [1, 0],  // 아래
    [0, 1],  // 오른쪽
    [0, -1], // 왼쪽
  ];

directions: 2차원 배열의 이동방향을 저장해둔 변수

arr2D[row][column]에서 탐색을 시작했을 경우 해당 좌표에서는 up, down, right, left의 근접 좌표를 방문합니다.

4. while 반복문 #

4-1. stack에서 값 꺼내오기 #

시작점인 (0, 0)의 좌표를 방문한 좌표로 체크합니다.

stack의 길이가 존재하는 경우 stack에서 현재 좌표, 그동안 이동한 path를 꺼내옵니다.

최초의 currentRow, currentCol는 각각 0, path는 빈 배열입니다.

  visited[0][0] = true;

  while (stack.length > 0) {
    const [[currentRow, currentCol], path] = stack.pop();
    // if (array[currentRow][currentCol] === 1) {
    //   return [...path, [currentRow, currentCol]];
    // }

    // ...
  }
  return null;

currentRow: 현재 방문한 좌표의 row 값
currentCol: 현재 방문한 좌표의 column 값
path: 축적된 좌표들의 배열 즉, 경로

4-2. 현재 방문한 좌표가 찾고자 하는 값인지 확인하기 #

stack에서 꺼내온 현재 방문한 2차원 배열의 좌표가 원하는 값인지 확인합니다.

그동안 축적한 path와 현재 방문 좌표를 배열에 담아 반환하고 함수는 종료됩니다.

  while (stack.length > 0) {
    // const [[currentRow, currentCol], path] = stack.pop();

    if (array[currentRow][currentCol] === 1) {
      return [...path, [currentRow, currentCol]];
    }

    // for ([dRow, dCol] of directions) { ... }
  }
  return null;

4-3. 방문한 좌표에서 directions만큼 탐색하기 #

DFS는 방문한 좌표(vertex, node 등)에서 주변을 탐색합니다. 탐색의 조건은 if문에 의해 더 탐색이 가능한 곳인지를 확인합니다.

newRow, newCol: 현재 방문한 좌표에 새 좌표값을 더합니다.
if문에 대해: 새로 정의된 좌표의 값이 0 미만이거나 rows, cols의 값을 넘는다면 배열의 인덱스 범위를 벗어나므로 무시합니다.
!visited[newRow][newCol]: 방문한적 있다면 무시합니다.

//   while (stack.length > 0) {
// ...
    for ([dRow, dCol] of directions) {
      const newRow = currentRow + dRow;
      const newCol = currentCol + dCol;
      if (
        newRow >= 0 && // 이동 할 좌표가 row의 최소값 보다 큰지 
        newRow < rows && // 이동 할 좌표가 row의 최대값 보다 큰지 
        newCol >= 0 && // 이동 할 좌표가 col의 최소값 보다 큰지
        newCol < cols && // 이동 할 좌표가 col의 최대값 보다 작은지
        !visited[newRow][newCol] // 이미 방문한 적 있는지
      ) {
        // 위 모든 if조건을 만족하면 [[다음 이동 할 row 좌표, 다음 이동 할 col 좌표], [현재까지 이동한 좌표들, [현재 row 좌표, 현재 col 좌표 ]]] 를 저장합니다.
        stack.push([
          [newRow, newCol],
          [...path, [currentRow, currentCol]],
        ]);
        visited[newRow][newCol] = true; // 이동 할 좌표의 방문을 체크
      }
    }
// }
// return null // 만약 못찾았다면 null을 반환

DFS의 이차원배열 탐색의 경로 #

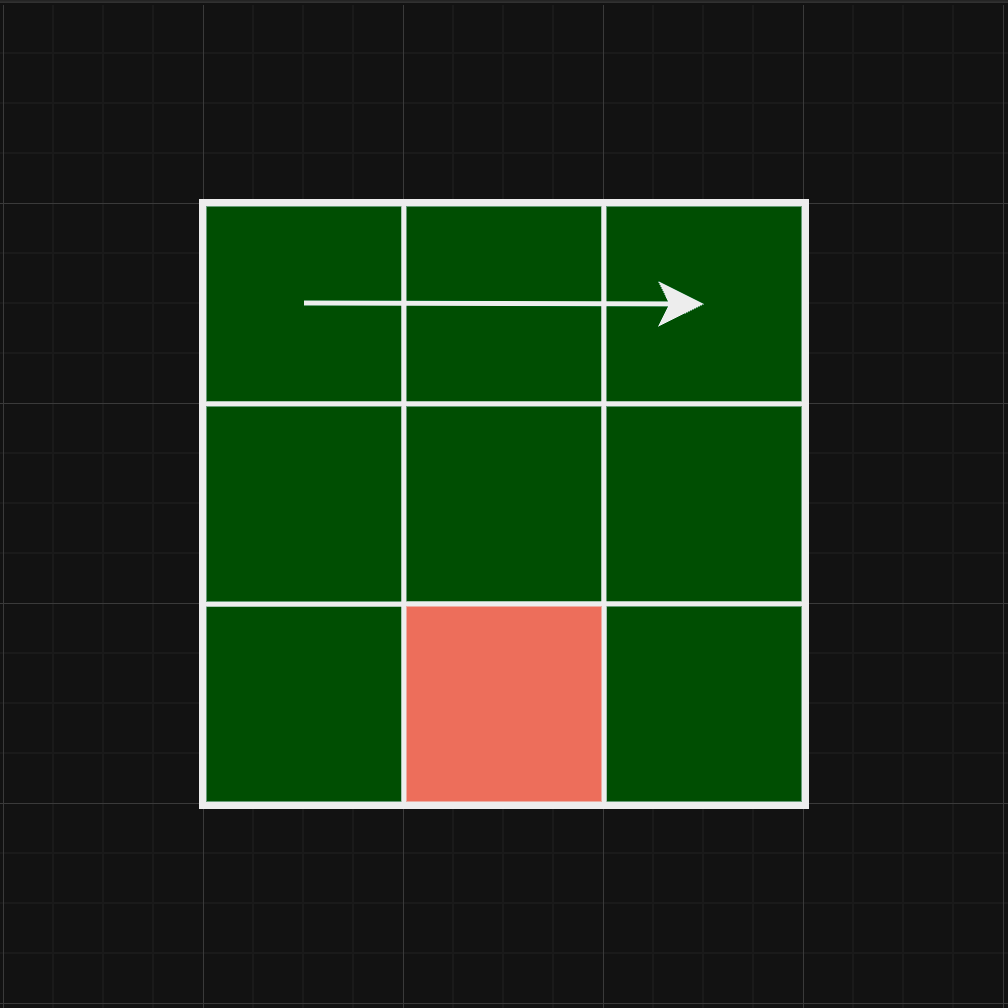
2차원 배열의 시작점인 (0, 0)에서 상하좌우 각 이동 가능한 루트를 탐색합니다.
탐색이 가능한 루트가 발견되면 예를 들어 (0, 0)에선 우측으로 탐색이 불가능 할 때까지 나아갑니다.

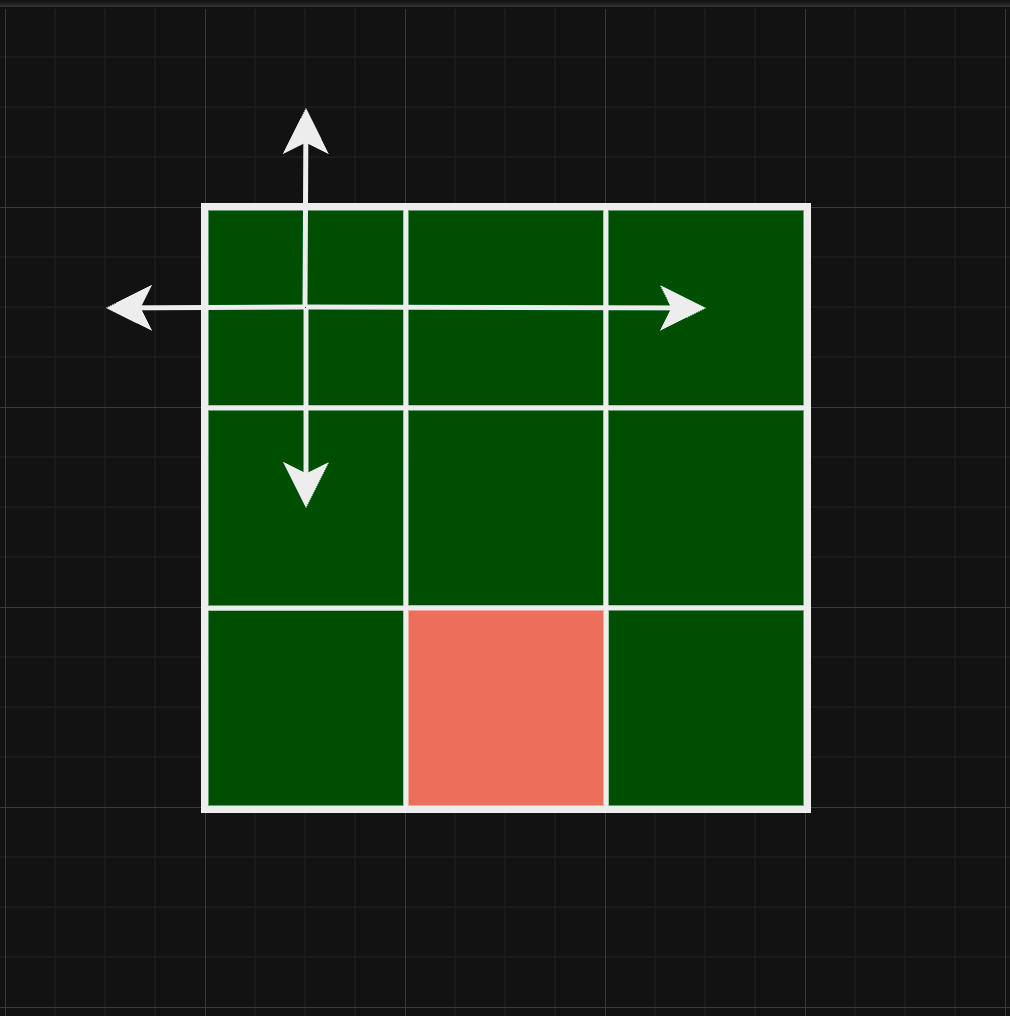
출발점이 (0, 0)일 때, 우측 뿐아니라 아래로도 길이 열려 있습니다. 그런데도 우측으로만 나아가는 이유는 현재 좌표에서 나아갈 방향을 정하는 directions와 stack에 이유가 있습니다.

directions는 순서대로 (0, 0)에서 이동 가능한 다음 좌표를 탐색합니다. 상하좌우에서 이동 가능한 영역은 directions 배열 순서대로 하, 우 입니다. 즉 아래와 우측을 이동 할 수 있다고 스택에 저장합니다. [하, 우].pop() // 우

스택은 pop으로 다음 행선지를 꺼내오기 때문에 우측 이동을 그 다음 행선지로 선택하게 됩니다.

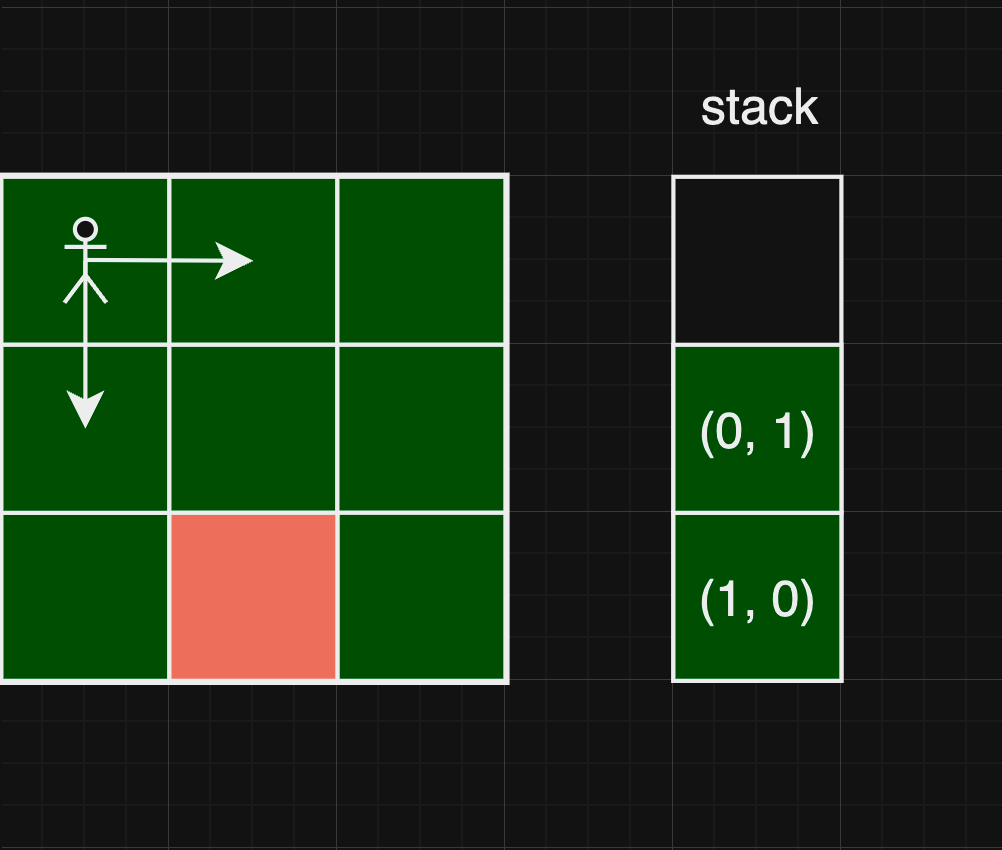
위와 같은 상황에서 stack은 pop이 되므로 다음 행선지는 (0, 1)이 됩니다.

만약 (0, 1)에 이동한 뒤 이동 경로가 모두 적절하지 않을 경우 반복문에 의해 stack은 pop되어 (1, 0)으로 돌아와 다음 행선지를 살펴보게 됩니다.

결론적으로 DFS로 이차원배열을 탐색하게 되면 목적지까지의 최단거리를 찾지는 않습니다.

대신 해당 목적지까지 계속 진행 가능성을 확인하며 나아갈 수 있습니다.

BFS로 2차원 배열 탐색하기 #

DFS에 이어, 너비 우선 탐색을 사용해 2차원 배열을 탐색하겠습니다. BFS는 최단 경로를 찾는 데 유리합니다.

이번에는 BFS로 동일한 배열에서 1을 찾아보겠습니다.

DFS에서 BFS로의 전환은 약간의 코드 변경만으로 가능합니다.

stack을 queue로 #

  const queue = [[[0, 0], []]]; // stack -> queue

이름만 변경되었을 뿐, 3차원 배열 객체입니다. (사실 자바스크립트의 배열은 dequeue에 가까워 양쪽 끝에서 추가, 삭제가 가능하기에 그냥 사용하면 됩니다.)

pop을 shift로 #

  visited[0][0] = true;

  while (stack.length > 0) {
    const [[currentRow, currentCol], path] = stack.shift();
    // if (array[currentRow][currentCol] === 1) {
    //   return [...path, [currentRow, currentCol]];
    // }

    // ...
  }
  return null;

이로써 최단 경로를 찾는 BFS를 만들게 되었습니다.

이제 변경이 왜 DFS에서 BFS로 바뀌는지 알아보겠습니다.

차이점 #

위 이미지를 통해 stack의 pop을 통해 다음 이동할 좌표를 가져온다는 것을 확인했습니다.

이제 자료구조가 queue이므로 값은 shift로 가져옵니다.

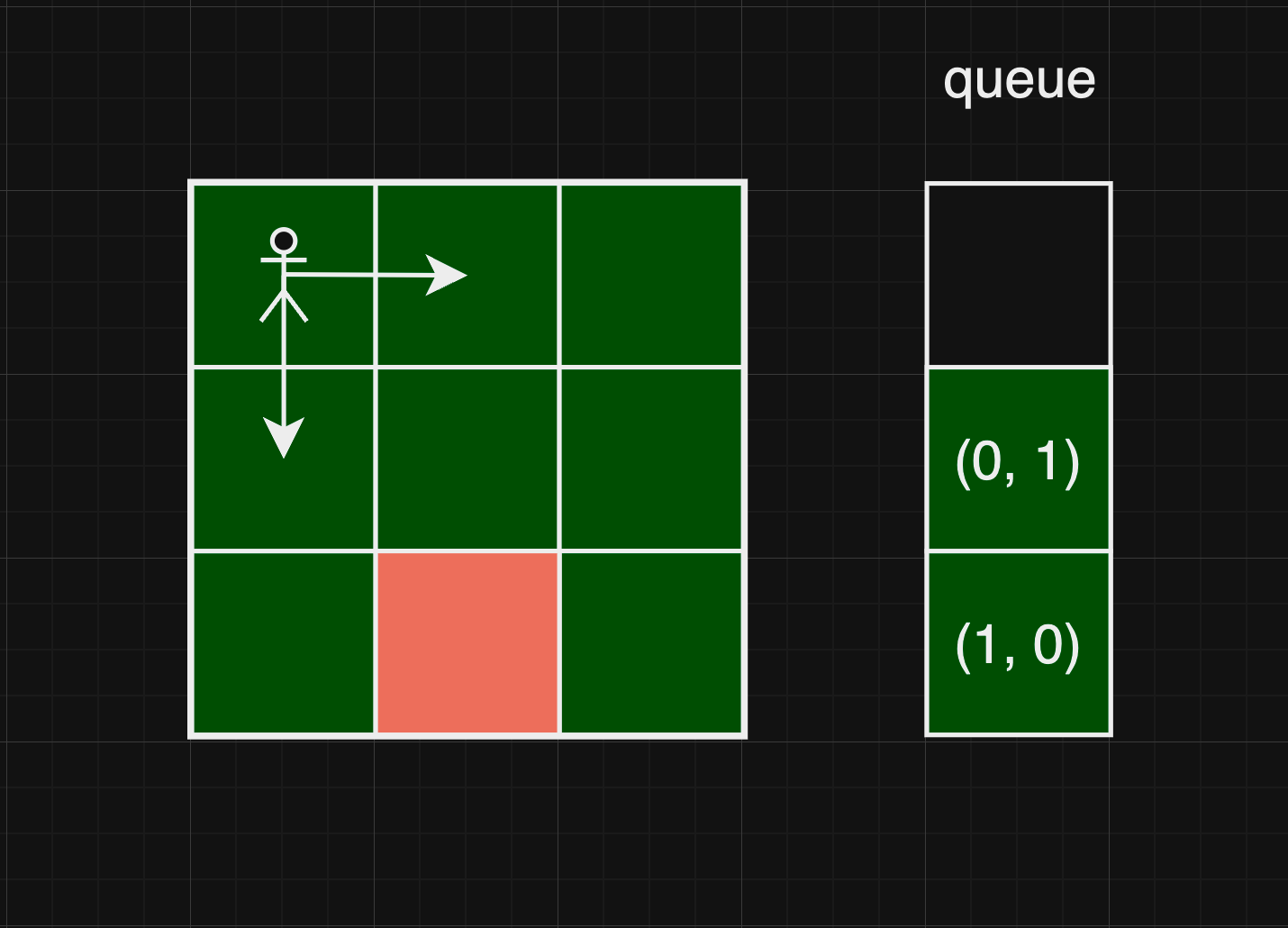
따라서 다음 이동 할 좌표는 (1, 0)입니다. 이 때, (1, 0)에서 이동 가능한 좌표 (1, 1), (2, 0)을 push합니다.

이 때 queue = [(0, 1), (1, 1), (2, 0)]

그 후, 다시 shift로 값을 꺼내오기 때문에 (0, 1)의 위치에서 이동가능한 좌표를 쌓아갑니다.

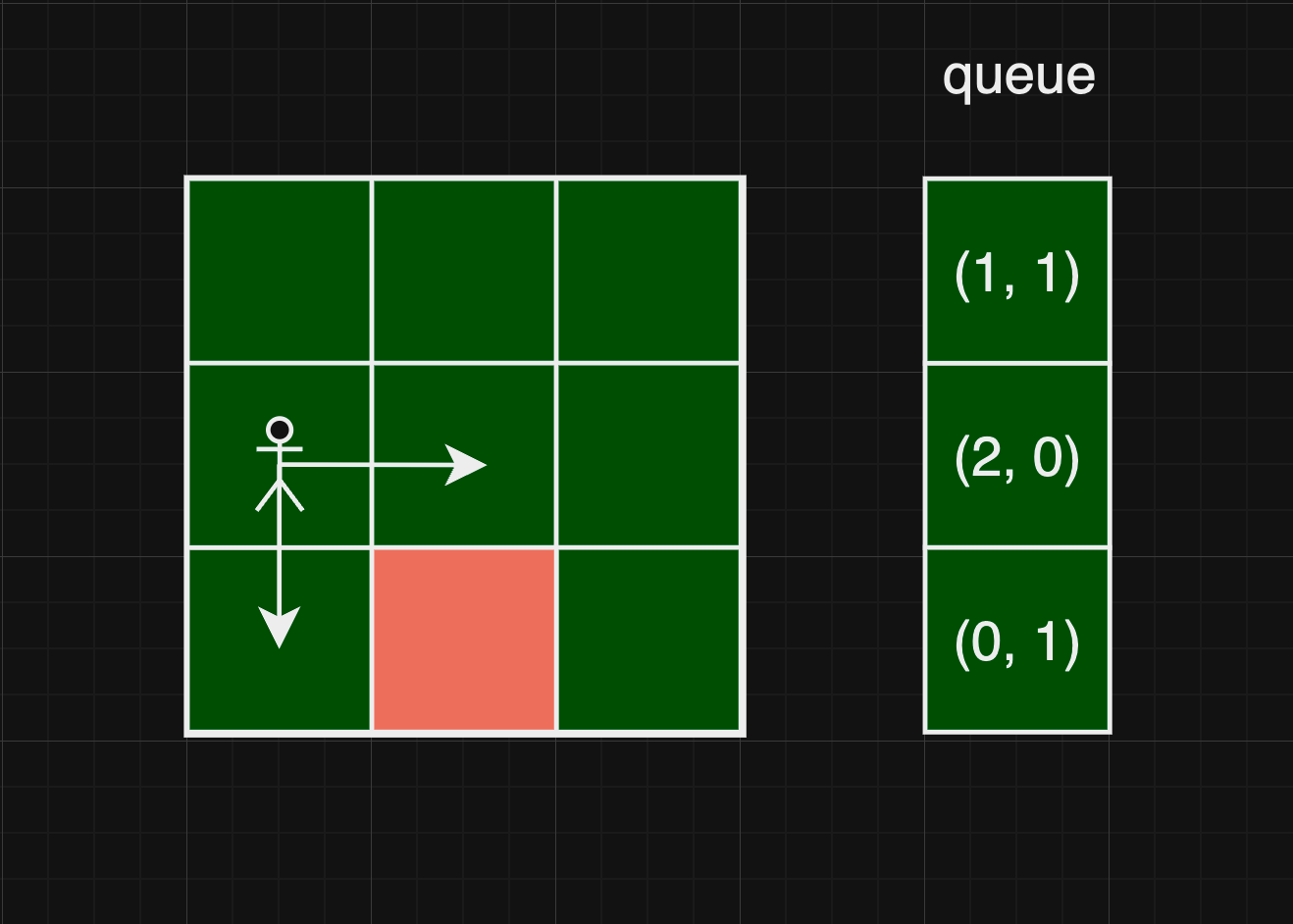
이를 반복하게 되면 처음 (0, 0)에서 탐색한 좌표를 입력된 순서대로 이동해서 가능한 이동 좌표들을 추가합니다.

즉, (0, 0) 부터 입력된 좌표를 하나씩 이동해보고 이동 가능한 좌표를 확인합니다. 이중 가장 먼저 1을 찾은 경로는 최단거리와 같습니다.

2차원 배열을 탐색하는 BFS, DFS