bottom up #
문제는 이전 게시글인 재귀 트리를 통한 접근에 있습니다.
- amount보다 하나 큰 배열을 만든다.
- amount를 순회한다.
- 순회하면서 각 인덱스의 값을 가진 coins만큼 순회한다.
- 이전 dp의 값에서 코인만큼 뒤에 있는 값을 꺼내와 하나를 더해 비교한다.
- 더 작은 값을 반환한다.
- dp 배열에 저장한다.
- 반복한다.
// java
int[] coins = {1, 2};
int amount = 3;위와 같은 코인 배열과 amount를 예로 들면,
amount + 1만큼 int 배열을 만듭니다.
// java
int[] dp = new int[amount + 1];dp배열의 각 인덱스를 인덱스의 값만큼 최소한의 코인으로 채운 코인의 수라고 합시다.
예를 들어
dp[0]은 index 0입니다. index 0을 코인의 amount로 본다면 amount 0은 코인 0개로 만들 수 있습니다.
dp[1]은 index 1입니다. index 1은 코인 1짜리 한개로 만들 수 있습니다. dp[1] = 1이 되야합니다.
dp[2]는 index 2입니다. index 2 는 코인 1 짜리 두개 혹은 2 짜리 코인 한개로 만들 수 있습니다. 그럼 둘 중 작은 값을 dp[2]에 넣어줍니다. dp[2] = 1 입니다.
이런 식으로 값을 채워나가는 것입니다.
여기서 중복계산이 숨어있다는 것을 어렴풋이 느낄 수 있습니다. 바로 dp[2]에는 dp[1]의 값을 활용 할 수 있다는 것입니다.
// java
int[] coins = {1, 2};
int amount = 3;아래와 같이 이중 반복문을 만듭니다.
int[] coins = {1, 2};
int amount = 3;
for(int i = 0; i < coins.length; i ++) {
for(int coin : coins) {
// 아직 빈칸
}
}amount는 3이네요.
소유한 코인으로 0을 만드는 경우를 포함하기 위해, 3 보다 하나 큰 배열을 만들고 해당 배열을 4로 초기화 하겠습니다.
// java
int[] coins = {1, 2};
int amount = 3;
int[] dp = new int[amount + 1]; // [0, 0, 0, 0]
Array.fill(dp, amount + 1); // [4, 4, 4, 4]
dp[0] = 0; // [0, 4, 4, 4]
for(int i = 0; i < coins.length; i ++) {
for(int coin : coins) {
// 아직 빈칸
}
}dp[0]의 값은 아무 코인도 넣지 않으면 되고 이미 dp[0] = 0;을 통해 값을 초기화 했으므로
적절한 조건문을 통해 넘어가줘야 합니다.
// java
// ...
for(int i = 0; i < coins.length; i ++) {
for(int coin : coins) {
if(i - coin < 0) continue;
}
}coin만큼 뒤에서 값을 꺼내오기 #
dp 배열에 접근 할 수 있으려면 i - coin의 값은 0 이상이여야 합니다.
i - coin은 외부 반복문이 dp를 순회하며 이전 dp[i - coin]의 값을 가져오는데도 사용됩니다.
dp[i-coin]은 dp 배열에 저장한 각 dp 배열의 index 만큼을 coins로 달성하기 위해
최소 몇개가 필요한지를 저장한 저장소입니다.
dp[i-coin]으로 접근한다는 것은 현재 dp index에서 지금 순회하고 있는 coin만큼
뒤로 이동한다는 것인데요
coin만큼 뒤로 이동한 결과값에 + 1을 한 경우 이전의 결과값에 수중의 코인 한개를 더하면 dp에 값을 채워넣을 수 있다는 것입니다. (특정 코인이 아닌 코인 한개!)
아래는 디버깅 중인 값을 추출해왔다고 생각해주세요
dp[0] = 0;
// 아래는 반복문
dp[2] = Math.min(dp[2]/** 4 */, dp[2 - 1] /** 1 */ + 1) // 반복문 coin = 1 일 때,
dp[2] = Math.min(dp[2] /** 2 */ , dp[2 - 2] /** 0 */ + 1) // 반복문 coin = 2 일 때coins로 내부에서 반복문이 다시 돌기 때문에 위와 같은 상황이 만들어집니다.
coin = 1일 때 dp에서 코인 1 만큼 이전 데이터 값을 불러옵니다. dp[2 - 1]이겠네요 이 값은 1이죠 이 값에 코인 1을 더하면 2가 되므로 dp[2]의 값 4와 비교하면 더 작은 값으로 저장됩니다.
이 방식은 dp에서 순회중인 코인만큼의 이전 값을 꺼내와 해당 값에 해당 코인을 하나 더하면 최소 값을 만족하는 것을 이용한 것입니다.
package leetCodes;
import java.util.Arrays;
public class CoinChangeIterate {
public static void main(String[] args) {
int[] coins = {1,2};
int amount = 3;
int result = coinChange(coins, amount);
System.out.println("result: " + result);
}
public static int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
Arrays.fill(dp, amount + 1);
dp[0] = 0;
for(int i = 0; i < dp.length; i++) {
for(int coin : coins) {
if(i - coin < 0) continue;
dp[i] = Math.min(dp[i], 1 + dp[i - coin]);
}
}
return (dp[amount] == amount + 1) ? -1 : dp[amount];
}
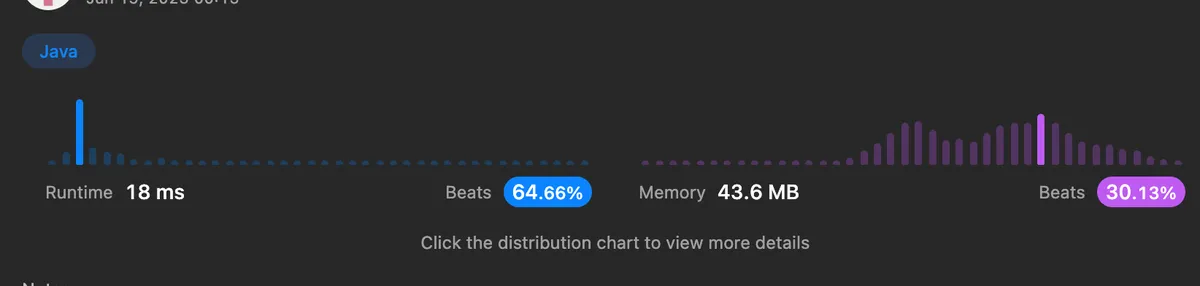
}위 알고리즘의 성능입니다.
요약 #
bottom-up 방식의 핵심은 이전 값들에서 새로운 값을 뽑아낸다는 것입니다. 위 문제에선 이전 값을 찾아가는 방식이 핵심입니다.
보통 bottom-up 방식은 각 배열의 index에 해당하는 값이 각 문제의 정답을 가지고 있습니다.
n번째 문제를 구하기 위해 n - coin번째의 값을 꺼내오는 것입니다.
만약 n - coin번째의 값에 답이 없다면 처음 Array.fill 메서드로
초기화한 값이 반환되게 되므로 해당 값은 amount + 1의 값이므로
최대값을 항상 넘게 됩니다.
이렇게 적고 보니 너무 장황한 글이 되었습니다.
퇴고를 반복해 글을 다듬어보겠습니다.
최적화 #
중첩된 반복문을 아래와 같이 변경해보세요

for (int coin : coins) {
for (int i = coin; i <= amount; i++) {
dp[i] = Math.min(dp[i], 1 + dp[i - coin]);
}
}위 반복문은 이전 풀이와 사뭇 다릅니다.
dp[i]의 값이 가지는 의미는 같습니다만, 필요없는 초반 탐색을 많이 개선했습니다.