동전 교환 문제 - 재귀

동전 교환 문제 #

각 동전의 개수가 무한한 동전과 거슬러 줘야 하는 값이 있습니다. 각각 coins, amount로 표현해보겠습니다.

// java
int[] coins = {1, 2, 5};
int amount = 5;

동전을 amount 만큼 거슬러 줘야 합니다.

단, 가장 최소한의 동전 갯수를 사용해 거슬러주면 됩니다.

위 조건의 경우 동전 5짜리를 하나가 최소한의 갯수를 충족하므로 정답은 1입니다.

시작하기 전에 #

이 문제를 풀기에 앞서 이해하면 좋을 내용들

• 트리에 대한 이해
• DP에 대한 이해

트리에 대한 이해 #

텍스트보단 아래와 같은 이미지가 설명에 훨씬 도움이 될 것입니다.

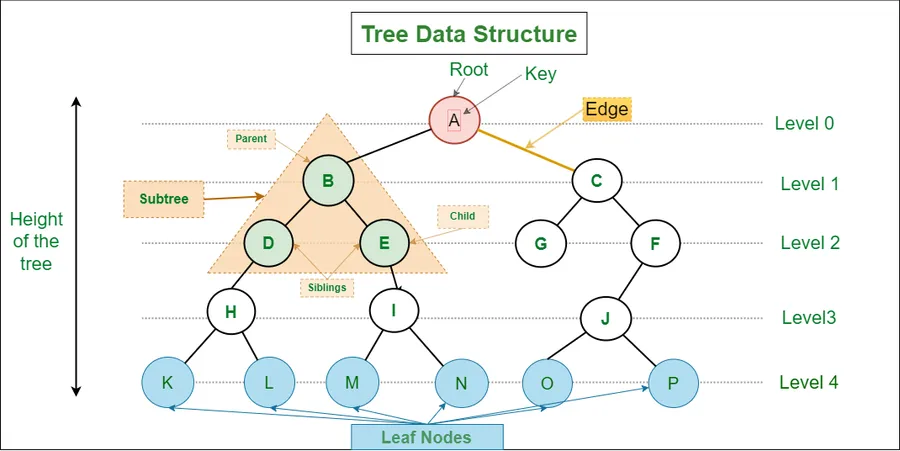
DP에 대한 이해 #

이 문제는 최적 하위 구조를 가지므로 동적 계획법 문제이다. 이런 문구를 어디선가 본 적이 있을겁니다.

이 문제를 예로 최적 하위구조를 설명해보겠습니다.

거스름돈을 거슬러 줄 때 정해진 n개의 종류로 (각 동전의 갯수는 무한인) 거스름 돈을 돌려주면 됩니다. 최소한 몇 개의 동전이 필요한지를 구하는 문제이므로

최적 하위구조에 적합하단 말인데 이 것만으로는 이해가 어렵습니다.

극단적으로 문제를 쉽게 만들어 이해력을 높여보겠습니다.

// java
int[] coins = {1, 2};
int amount = 3;

• 거슬러 줄 수 있는 코인은 2개
• 거슬러 줘야 하는 값은 3입니다.

1짜리 코인으로 amount를 3만큼 거슬러주겠습니다.

(((amount - 1) - 1) - 1) = 0 같은 함수를 3번 중첩합니다. 이는 재귀 함수이자 합성 함수이죠 3번 함수를 실행하면 amount는 0이 됩니다.

0이 된 값은 기저조건에 닿게됩니다. 이렇게 한 번의 조건을 찾아냈습니다.

이는 재귀 트리의 왼쪽 노드만 타고 내려온 결과입니다.

만약 이 왼쪽 최외각 리프 노드에서 바로 위 레벨로 올라가 다시 오른쪽 노드로 내려간다면 2짜리 코인으로 amount를 빼서 amount의 값은 -1입니다.

이렇게 왼쪽 노드만 타고 내려간 결과와 그 옆에도 한번 다리를 걸친 결과가 서로 아무 영향을 주지 않기 때문에 최적 하위 구조라고 할 수 있습니다.

문제 #

1. k개의 서로 다른 종류의 동전이 있습니다.
   1. 예시로 3개라면 1 동전, 2 동전, 5 동전 각각 종류가 다릅니다. 각각의 동전은 무한합니다.
2. amount가 있습니다. k개의 동전을 최소한으로 사용해 amount 만큼 거슬러주면 됩니다.

동전 배열 {1, 2, 5} 가 주어지고 11이라는 amount가 주어지면 5 + 5 + 1로 3개의 동전을 사용해 amount만큼 거슬러 줄 수 있으므로 답은 3이 됩니다.

경우의 수 문제를 재귀로 풀기 #

이 문제는 재귀 호출을 반복문 속에서 호출해 각 단계에서 일어날 수 있는 경우의 수를 재귀적으로 탐색해 문제를 풀이합니다.

// java
		for (int coin : coins) {
			int subProblem = dp(coins, amount - coin);
			// ...

반복문을 코인만큼 순회합니다.

현재 코인은 {1, 2}라고 한다면 루트에서 서브트리는 크게 3 - 1, 3 - 2를 키로 하는 서브트리가 생겨나게 됩니다.

반복문 속에 재귀 호출이 일어나게 되면 보통 이런 패턴을 따르게 됩니다.

코드의 흐름에 따라 재귀를 그려나가 보겠습니다.

루트인 3에서

• 기저조건을 확인합니다.

• 루트에서 코인 1만큼을 제합니다.

그리고 다시 재귀 호출이 일어나게 됩니다.

• 기저조건을 확인합니다.

• 2에서 코인 1만큼을 제합니다.

그리고 다시 재귀 호출이 일어나게 됩니다.

• 기저조건을 확인합니다.

• 1에서 코인 1만큼을 제합니다.

• 기저조건을 확인합니다.

기저조건인 amount == 0을 만족하게 되었습니다.

부모 트리에 0을 반환합니다.

재귀 함수에서 기저 조건과 기저 조건이 반환하는 값은 알고리즘의 답을 반환하는 과정입니다.

저희가 풀고 있는 단순하게 변경한 형태를 더욱 쉽게 변경해서

// java
int[] coins = {1};
int amount = 3;

이러한 조건을 가진 문제로 변경했다고 하면 문제는 이미 다 풀어낸 것과 마찬가지입니다.

amount라는 값은 재귀 호출을 통해 코인 1로 값을 제하면서 다음 호출 스택에 값을 넘겨주게 됩니다. 3 -> 2 -> 1 -> 0 이런 식으로 말이죠

해당 문제에서 구하고자 하는 것은 잔돈을 얼만큼 거슬러 주는지 카운트 하는 것입니다.

따라서 기저 조건을 만족한 값을 제외한 모든 간선의 합을 구하면 해당 문제의 답을 찾게 되는 것입니다.

단 이러한 질문이 생겨나게 됩니다.

Q: 그 다음 코인에 대한 경우의 수를 제외하면 당연히 그렇게 되는 것이다. 🤔

맞습니다.

이런식으로 문제에 대한 해답을 올바른 방향으로 이끌게 하는 질문을 던지고, 그에 대한 대응을 하는 것으로 알고리즘의 정답에 가까워지는 것이 이 문제 풀이에 대한 이해를 높이는 접근법입니다.

계속하자면 하나의 하위 문제에 대한 해답을 찾았습니다. 3 -> 2 -> 1 -> 0에서 기저 조건을 제외한 간선수를 세면 그것이 해당 루트를 통한 거스름 돌려주기에 대한 해입니다.

만약 3 -> 2 -> 1의 시점에 코인 2를 주는 경우를 생각해봅시다.

3 -> 2 -> 1 -> -1이라는 계산이 되죠 이러면 거스름돈을 원래 값보다 더 많이 주게 되어 해당 경우는 카운트 하지 않아도 됩니다.

새로운 조건을 찾아냈습니다.

나아가 한가지 더 생각할 수 있습니다.

3 -> 2 에서 코인 2짜리를 주는 경우입니다. 3에서 1만큼, 2에서 2만큼 코인을 주면 총 2개로 코인의 수가 거스름돈의 코인 수는 3 -> 2로 줄어들게 됩니다.

저희가 하나씩 짚어가며 살펴본 루트는 가장 왼쪽의 3 -> 2 -> 1 -> 0으로 뻗어나가는 경우입니다.

이를 경우 1이라고 하겠습니다.

그리고 3 -> 2 -> 0 코인 1짜리와 2짜리를 순서대로 주어 코인 2개로 거슬러주는 경우의 수를 보았습니다.

이를 경우 2이라고 하겠습니다.

그림으로 보면 아래와 같습니다.

레벨 1의 노드 2에서 경우 1과 경우 2의 결과 값이 모이게 됩니다.

코인 1을 3번 쓴 경우 1의 결과 값은 3입니다.

코인 1, 2를 섞어 사용한 경우 2의 결과 값은 2입니다.

이제 상위 노드에 경우 1과 경우 2를 비교해 작은 값을 반환하면 됩니다. 아래 코드가 바로 그런 코드입니다.

// java
			...
			if (subProblem == -1) continue;
			res = Math.min(res, 1 + subProblem);
		}

		if (res != Float.POSITIVE_INFINITY) {
			return (int) res;
		}
		return -1;
	}

마지막으로 -1을 반환하는 서브트리에 대한 처리입니다.

해당 서브트리는 결과값을 내지 못했으므로 무한대의 값을 상위 루트에 올립니다.

서브트리의 반환값은 서브트리의 부모 트리가 받게 되는데 해당 값은 다시 비교되어 적은 값을 부모트리에 올립니다.

// java
		float res = Float.POSITIVE_INFINITY;

이제 모든 설명이 끝났습니다. 😆

풀이 #

아래의 재귀트리는 주어진 코인 배열을 순회하면서 각 코인을 통해 재귀 함수를 실행합니다.

• 재귀 함수의 기저조건은 amount = 0이 되었을 때 0을 반환합니다.
• amount의 값이 0 보다 작은 경우 -1을 반환합니다. 해당 재귀의 결과는 유효하지 않다는 정보를 나타냅니다.

// java

package leetCodes;

public class CoinChange {
	public static void main(String[] args) {
		int[] coins = {1, 2, 5};

		int result = dp(coins, 11);
		System.out.println("result: " + result);
	}

	static int dp(int[] coins, int `amount`) {
		// base case
		if (amount == 0) return 0; // 딱 맞아 떨어지는 경우
		if (amount < 0) return -1; // 초과하는 경우

		float res = Float.POSITIVE_INFINITY;

		for (int coin : coins) {
			int subProblem = dp(coins, amount - coin);

			if (subProblem == -1) continue;
			res = Math.min(res, 1 + subProblem);
		}

		if (res != Float.POSITIVE_INFINITY) {
			return (int) res;
		}
		return -1;
	}


}

이런 문제는 재귀 트리를 그려보면 이해가 쉬운데요

꼭 자기 손으로 그려보는게 좋습니다.

아래는 위 재귀트리를 통한 문제풀이를 UML을 사용해 나타낸 것입니다.

단계를 나누어 하나씩 음미하는 시간을 가지겠습니다.

마무리 #

재귀는 컴퓨터에 무한한 속도와 자원이 있다면 거의 모든 문제를 해결 할 수 있는 만능키와 같습니다. (모든 경우를 무한한 속도로 찾으면 되니까요! 🤖)

재귀가 나타내는 트리와 그 트리를 탐색하는 방법,

재귀 함수가 반환한 결과값이 어디로 이동하는지,

반환된 값들 끼리의 비교

이 모든 것을 알게 되면 최적화를 할 수 있는 빈틈이 보이게 되리라 믿습니다.

긴 글 봐주셔서 감사합니다.