rational function graph를 갈라보자 #

$P(x) = \frac{A(x)}{B(x)} = C(x) + \frac{A'(x)}{B(x)}$

식보다는 예제를 보는 것이 이해하기 좋습니다.

$f(x) = \frac{x^2+1}{x}$ 이러한 식이 있다고 하죠,

$$f(x) = \frac{x^2+1}{x} = \frac{x^2}{x} + \frac{1}{x} = x + \frac{1}{x}$$

각 항을 각각의 함수로 보면 일차함수와 유리함수 하나씩으로 나눠집니다.

일차함수의 그래프 h(x) #

$$h(x) = x$$

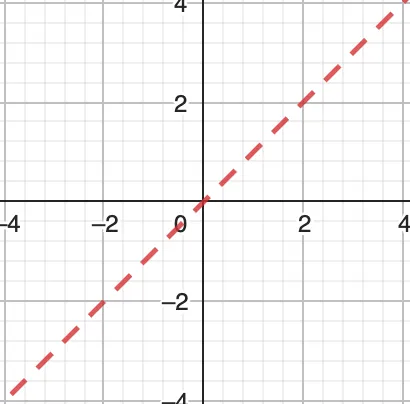
유리함수의 그래프 g(x) #

$$g(x) = \frac{1}{x}$$

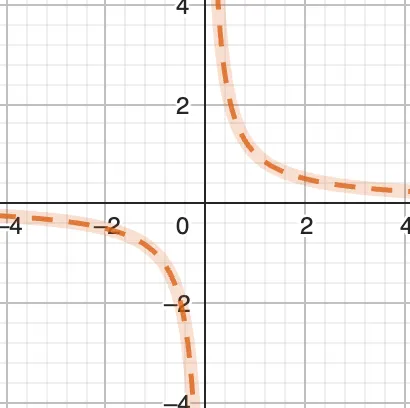
이 둘을 더한 함수는 어떤 그래프일까요? #

$$f(x) = h(x) + g(x)$$

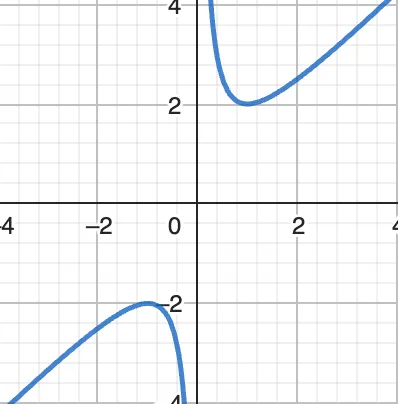
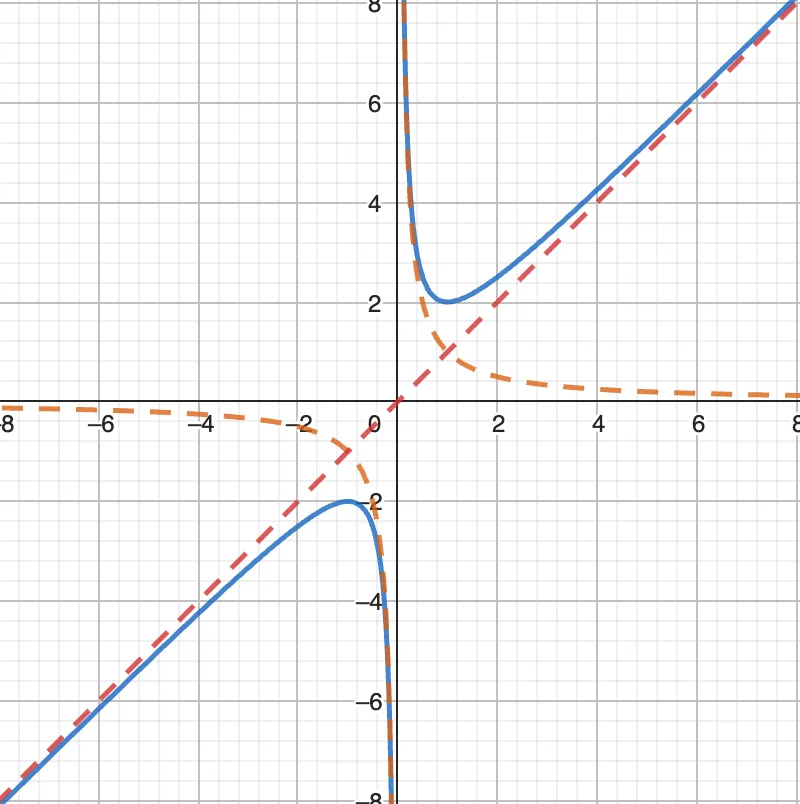
곂쳐서 보면 보이는 #

함수 $f(x) = h(x) + g(x)$는 유리함수 그래프 $g(x)$의 점근선이 일차함수 $h(x)$ 를 따라가고 있다는 것을 알 수 있습니다.