하노이의 탑이란? #

하노이의 탑(Tower of Hanoi)은 퍼즐의 일종이다. 세 개의 기둥과 이 기둥에 꽂을 수 있는 크기가 다양한 원판들이 있고, 퍼즐을 시작하기 전에는 한 기둥에 원판들이 작은 것이 위에 있도록 순서대로 쌓여 있다.

wikipedia

하노이의 탑의 규칙

한 번에 한개의 원판만 옮길 수 있다.
가장 위에 있는 원판만 이동할 수 있다.
큰 원판이 작은 원판 위에 있어서는 안 된다.

DP 관련 서적들을 뒤적이다 보면 꼭 등장하는 단골 손님인 하노이의 탑 문제입니다.

하노이의 탑 문제를 분석해봅시다.

분석 #

하노이의 탑 문제는 하위문제로 상위 문제를 해결 할 수 있습니다.

그 이유를 예제를 통해 알아보겠습니다.

예제 #

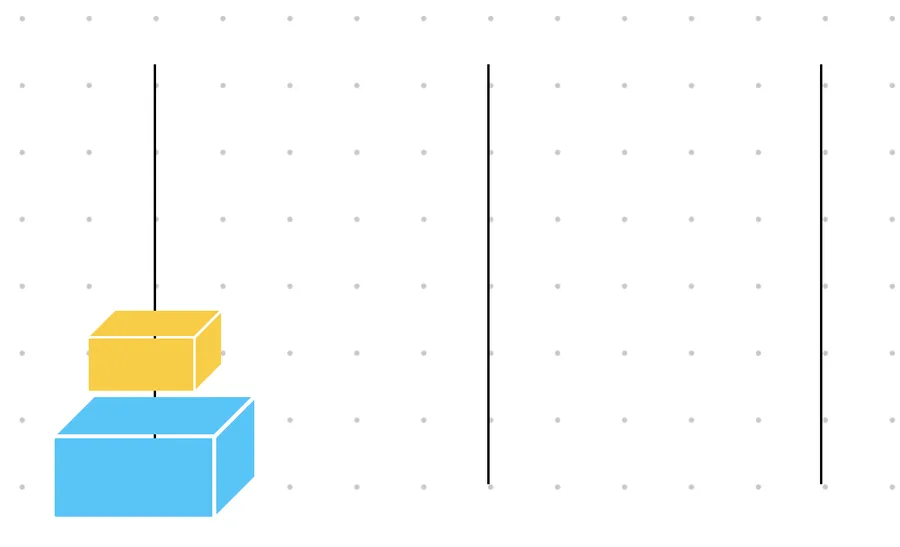
n = 2인 하노이의 탑은 이런 모양으로 시작하게 됩니다. 탑의 순서대로 s, d, e로 각각 이름을 지어줍니다.

s = start, d = destination, e = extra입니다.

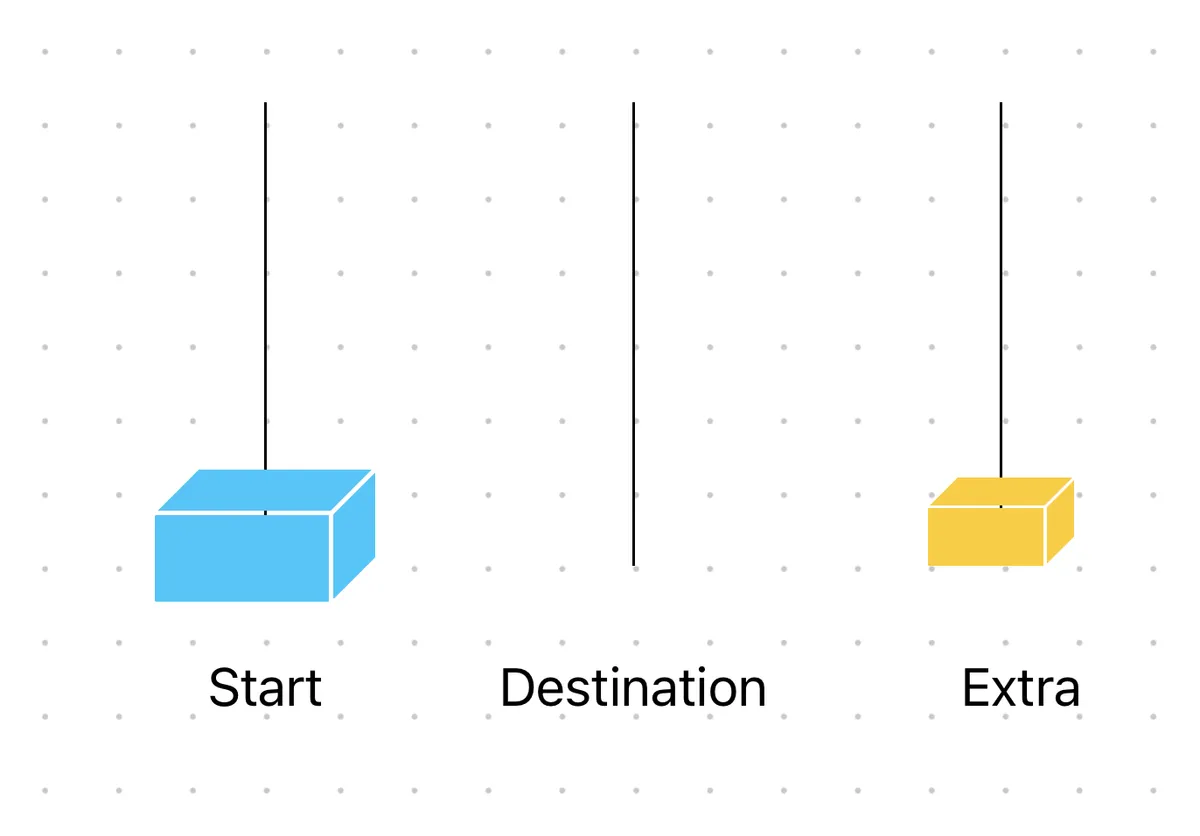
n - 1 개의 원판을,
탑 "d"를 이용해,
탑 "e"에 옮겨놓았다고 가정합시다.

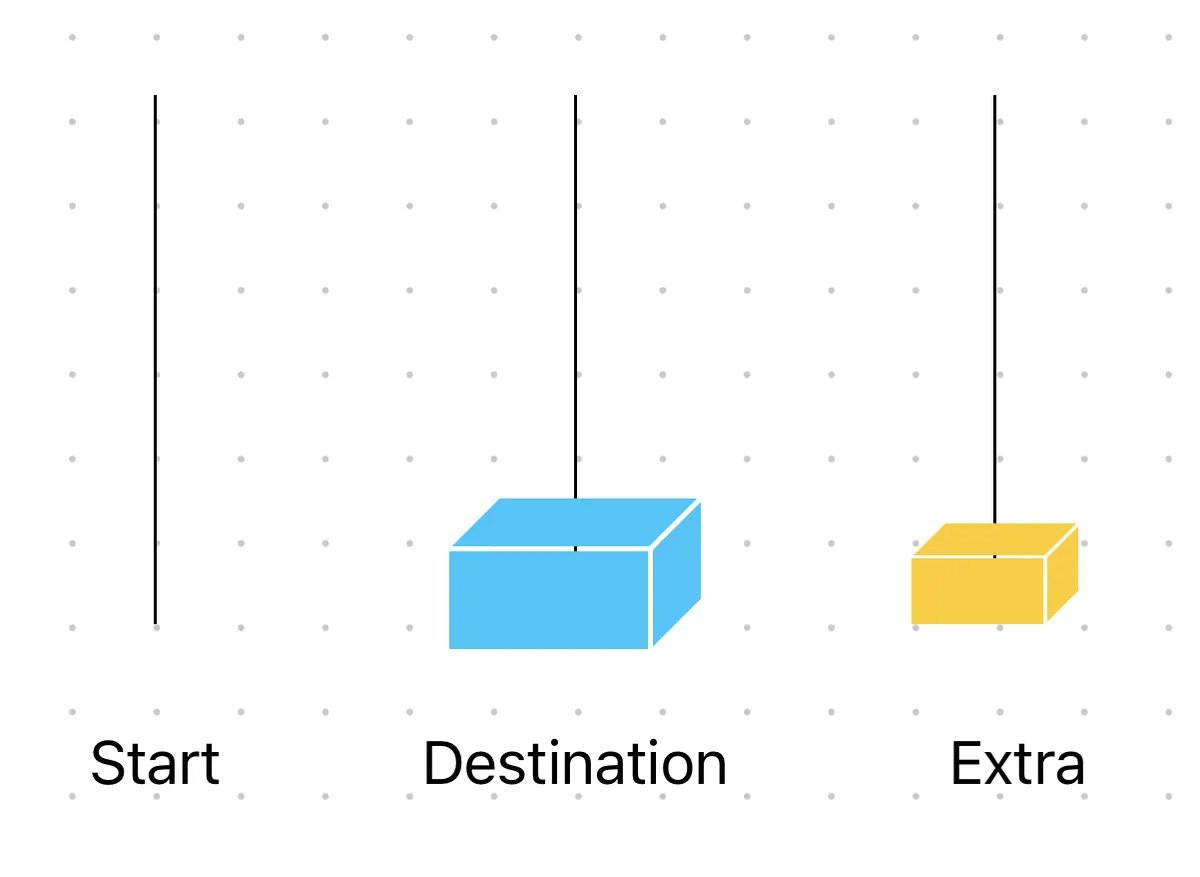
n 번째 원판을 d에 옮겨줍니다.

n 번째 원판은 가장 큰 원판을 가리킵니다.

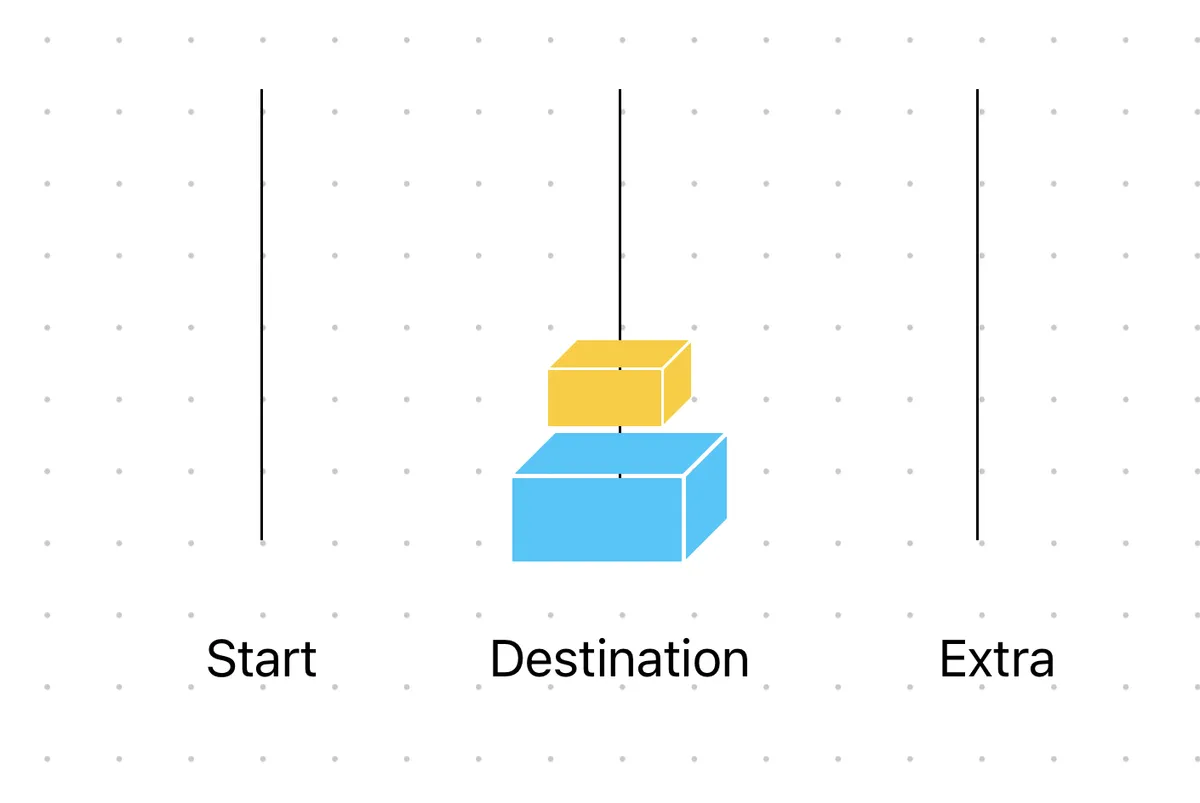
n - 1 개의 원판을,
탑 "s"를 이용해,
탑 "d"에 옮겨놓습니다.

구현 #

하노이의 탑 구현은 아래와 같습니다.

// javascript
function hanoi(s, d, e, n = 3){
    if(n <= 0) return;

    hanoi(s, e, d, n - 1);
    console.log(`${n} 번째 원판을${s}에서 ${d}로 이동`);
    hanoi(e, d, s, n - 1);
}

실행은 아래와 같습니다.

hanoi('s', 'd', 'e', 3);

기저조건 #

// javascript
function hanoi(s, d, e, n = 3){
    if(n <= 0) return;  // 기저조건입니다.
    // ...
}

기저조건은 n <= 0입니다.

n은 원판의 번호를 나타냅니다.

0 번째 원판은 원판이 모두 소진되어 바닥을 봤다는 의미입니다.

함수의 각 부분을 나누어 이해하겠습니다.

경유지 탑으로의 재귀 호출 #

// javascript
function hanoi(s, d, e, n = 3){
    // ...
    hanoi(s, e, d, n - 1); // 재귀 호출
    // ...
}

이 호출을 이해하기 위해서는 두가지 설명이 필요합니다.

재귀 호출 인자의 순서가 바뀐 것
호출의 이유

1번을 설명하면 2번도 자연스레 설명됩니다.

재귀 호출의 순서가 바뀌었죠 이는 탑의 순서가 바뀐 것입니다.

함수의 각 인자는 아래의 예시처럼 인자의 위치(탑의 이름이 아닌)에 따라 역할을 정할 수 있습니다.

// javascript
/**
 * @param {string} s 원판이 쌓인 장소 (출발 탑)
 * @param {string} d 원판이 쌓인 장소로부터 이동 할 탑 (목적지 탑)
 * @param {string} e 원판을 목적지로 이동시키기 위해 필요한 (경유지 탑)
 * @param {number} n 원판의 수
 * */
function hanoi(s, d, e, n = 3){
    // ...
}

그림을 통해 확인한 바로는

n - 1까지의 원판들을 목적지로 이동시키기 위해선 먼저 n - 1까지의 원판들을 경유지 탑까지 이동 시켜야합니다.

hanoi함수의 첫 인자는 출발 탑,
두 번째 인자는 목적지 탑,
세 번째 인자는 경유지 탑,
네 번째 인자는 원판의 번호입니다.

여기서 순서는 중요합니다.

첫번째 인자에 d를 넣고,
두번째 인자에 e를 넣고,
세번째 인자에 s를 넣으면

이렇게 해석됩니다.

탑 d에서 탑 s를 이용해 탑 e로 원판들을 옮긴다.

위 규칙에 따라 재귀 호출을 시작할 때 n - 1번째 까지의 원판을 경유지 탑으로 옮기기 위해

목적지 탑 인자의 위치에 경유지 탑을, 경유지 탑 위치에 목적지 탑을 넣은 것입니다.

실행하기 #

// javascript
function hanoi(s, d, e, n = 3){
    // ...
    console.log(`${n} 번째 원판을 ${s}에서 ${d}로 이동`);
    // ...
}

재귀호출을 돌다가 원판을 이동시킵니다.

인자 d는 재귀호출 인자의 순서를 변경하면서 바뀔 수 있다는 것을 이미 언급했습니다. d는 변수이고 안의 내용물은 바뀌게 됩니다.

목적지 탑으로의 재귀 호출 #

// javascript
function hanoi(s, d, e, n = 3){
    // ...
    hanoi(e, d, s, n - 1);
}

위의 재귀호출 인자의 순서가 가진 규칙에 따르면

탑 e에 있는 원판들을 탑 s를 이용해 탑 d로 이동시킵니다.

의문점 #

가장 큰 의문점은 이렇게 풀어봤자 이해가 가지 않는다는 치명적인 단점이 있습니다.

// javascript
function hanoi(s, d, e, n = 3){
    if(n <= 0) return;

    hanoi(s, e, d, n - 1);
    console.log(`${n} 번째 원판을 ${d}로 이동`);
    hanoi(e, d, s, n - 1);
}

hanoi("s", "d", "e", 2);

n을 2로 실행횟수를 줄여 이해 해봅시다.

첫 재귀는 인자의 d와 e의 순서를 서로 변경합니다. 아래와 같은 인자로 함수를 호출합니다.

hanoi("s", "e", "d", 1);

그럼 다시 시작된 hanoi 함수의 인자는

// javascript debugger
s: s,
d: e,
e: d,
n: 1

위의 상태가 됩니다.

기저조건을 통과하고 다시 재귀함수를 만나게 됩니다.

함수의 인자를 아래와 같이 넘겨줄 것입니다.

// javascript
hanoi('s', 'd', 'e', 0);

다시 첫 재귀 호출을 하던 인자로 넘겨주고 있습니다. 기저조건에 닿아 위 함수의 실행하기 부분은 무시되겠지만 실행된다고 가정한다면

s 탑에 있는 0번째 원판을 꺼내 d로 옮긴다.입니다.

콜스택에 쌓인대로 정리하자면

hanoi("s", "d", "e", 0); // 무시됨
hanoi("s", "e", "d", 1); // 실행됨
hanoi("s", "d", "e", 2); // 실행됨

콜스택의 인자들을 보면 인자들의 순서가 반복됨을 알 수 있습니다.

실행되는 함수들의 실행부의 출력만 모아보면


// 1 번째 원반을 s에서 e로 이동시킵니다.
// 2 번째 원반을 s에서 d로 이동시킵니다.

인자의 입력 순서가 번갈아가며 반복되는 덕에 적절하게 각 탑에 원판을 올바른 순서로 분배했습니다.

기저조건에 닿았으니 함수들이 실행되었습니다.

그 다음은 목적지 탑으로의 재귀 호출입니다.

목적지 탑으로의 재귀 호출은 경유지 탑으로의 재귀 호출과 그 방식이 다르지 않습니다. 따라서 설명보다는 이 알고리즘의 프레임에 대해 언급하는 것이 낫겠습니다.

이 풀이의 골자는 재귀함수의 중위순회에 있습니다.

중위순회는 루트의 값을 순회중 출력이 중앙값에 도달했을 때 출력합니다.

따라서 가장 큰 원판을 출발 탑에서 목적지 탑으로 옮길 수 있는 것이고

경유지탑으로 옮겼던 원판들을 똑같은 방법을 통해 목적지 탑으로 옮길 수 있는 것입니다.

마치며 #

아주 재미있는 문제입니다.

처음엔 어려웠지만 여러번 되새길 수록 배울게 많은 문제입니다.

최적화 할 것도 많아보입니다.