집합에 대해 #
집합은 서로 같지 않은 종류의 object 모음이라고 할 수 있다. 예를 들면 아래와 같이 집합을 정의 할 수 있다.
프로그래밍에선 집합에 여러 객체를 집어 넣을 수 있으며 언어에 따라 함수나 클래스 혹은 코드 자체를 집어넣을 수도 있다.
집합을 표현하는 방법들 #
원소나열법 Enumerating elements (Roster form) #
Set Builder #
집합의 예시들 #
- 함수
- domain (정의역)
- 함수 f(x)의 입력이 될 수 있는 모든 x 값의 집합을 domain이라고 합니다.
- codomain (공역)
- 함수에 어떤 값을 대입한 결과가 될 수 있는 것들의 집합이다.
- 함수의 값에 해당하는 치역을 포함한다.
- 치역이 되지 못한 값들은 공역에 존재한다.
- range (치역)
- 함수의 값에 해당한다.
- 이 값들의 집합을 range라 한다.
- domain (정의역)
- 직선, 평면
- 일차함수는 그래프로 나타내면 직선이 되는데 이 직선은 점들의 집합이다.
- 따라서 일차함수의 치역들의 집합은 직선이라고 할 수 있다.
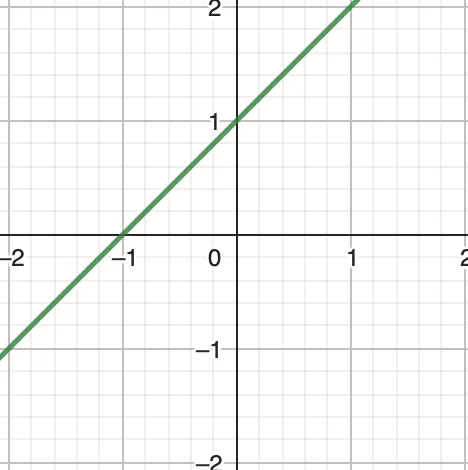
- 일차함수는 그래프로 나타내면 직선이 되는데 이 직선은 점들의 집합이다.
정리 #
집합의 기본적인 선언 방법을 알아봤습니다. 집합의 갯수가 적절히 적다면 나열법이 간단합니다만, 집합을 나열하기 어려운 경우 Set Builder를 사용합시다.